BTEC Level 3 Unit 7 Calculus to Solve Engineering Problems Assignment Brief
| University | Middle East College |
| Subject | Unit 7 Calculus to solve engineering problems |
Assignment Brief A
| Qualification | Pearson BTEC International Level 3 Extended Diploma in Engineering
Pearson BTEC International Level 3 Extended Diploma in Electrical/Electronic Engineering Pearson BTEC International Level 3 Extended Diploma in Mechanical Engineering Pearson BTEC International Level 3 Extended Diploma in Digital Engineering Pearson BTEC International Level 3 Extended Diploma in Manufacturing Engineering Pearson BTEC International Level 3 Extended Diploma in Aeronautical Engineering |
| Unit number and title | Unit 7: Calculus to solve engineering problems |
| Learning aim(s) | A: Examine how differential calculus can be used to solve engineering problems |
| Assignment title | Solving engineering problems that involve differentiation |
| Assessor | |
| Issue date | |
| Hand in deadline |
Vocational Scenario or Context
You are working as an apprentice engineer at a company involved in the research, design production and maintenance of bespoke engineering solutions for larger customers.
Part of your apprenticeship is to spend time working in all departments, however a certain level of understanding needs to be shown before the managing director allows apprentices into the design team and so she has developed a series of questions on differentiation to determine if you are suitable.
Task 1
Produce a report that contains written descriptions, analysis and mathematics that shows how calculus can be used to solve engineering problems as set out below.
(1)The equation for a distance, s(m), travelled in time t(s) by an object starting with an initial velocity u(ms-1) and uniform acceleration a(ms-2) is:
The tasks are to:
(a) Plot a graph of distance (s) vs time (t) for the first 10s of motion if and
(b) Determine the gradient of the graph at and .
(c) Differentiate the equation to find the functions for
i) Velocity ii) Acceleration
(d) Use your result from part c to calculate the velocity at and .
(e) Compare your results for part b and part d. 2 The displacement of a mass is given by the function
(2)
The tasks are to:
(a) Draw a graph of the displacement y(m) against time t(s) for the time to .
(b) Identify the position of any turning points and whether they are maxima, minima or points of inflexion.
(c) Calculate the turning points of the function using differential calculus and show which are maxima, minima or points of inflexion by using the second derivative.
Compare your results from parts b and c.
(3)The equation for the instantaneous voltage across a discharging capacitor is given by , where is the initial voltage and is the time constant of the circuit.
The tasks are to:
(a) Draw a graph of voltage against time for and , between and .
(b) Calculate the gradient at and .
(c) Differentiate and calculate the value of at and .
(d) Compare your answers for part b and part c.
(e) Calculate the second derivative of the instantaneous voltage .
(4)The same capacitor circuit is now charged up to 12V and the instantaneous voltage is .
The tasks are to:
(1) Differentiate with respect to to give an equation for
.43333w
Calculate the value of at and .
Find the second derivative .
(5) The gain of an amplifier is found to be ,:
The tasks are to find equations for:
(6) The displacement, (m), of a body in damped oscillation is
The task is to:
(a) Use the Product Rule to find an equation for the velocity of the object if .
(7) The velocity of a moving vehicle is given by the equation The task is to:
(a)Use the Chain Rule to determine an equation for the acceleration when .
(8) A communication signal is given by the function
The task is to:
(a) Derive and equation for using the Quotient Rule.
(9) A company is required to fence off the area around a robot arm to comply with health and safety law. They have 750m of fencing available
The task is to:
(a) Find the maximum area they can fence off?
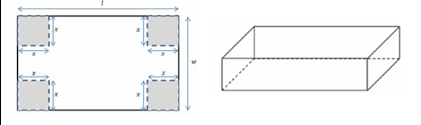
(10) You plan to make a simple, open topped box from a piece of sheet metal by cutting a square – of equal size – from each corner and folding up the sides as shown in the diagram:
If and calculate:
(a) The value of x which will give the maximum volume
(b) The maximum volume of the box
(c) Comment of the value obtained in part b.
Checklist of evidence required
Your informal report should contain:
- analysis
- worked solutions to the problems
Each worked solution should be laid out clearly and contain brief explanations of the stages of the calculation to indicate your understanding of how calculus can be used to solve an engineering problem. You explanation should be detailed in response to questions 9 and 10 to show how the variables are optimised in each case. Graphs should be well presented and clearly labelled and comparisons between methods should be accurate and well presented.
Criteria covered by this task: |
||
| Unit/Criteria reference | To achieve the criteria you must show that you are able to: | |
| 7/A.D1 | Evaluate, using technically correct language and a logical structure, the correct graphical and analytical differential calculus solutions for each type of given routine and non-routine function, explaining how the variables could be optimised in at least two functions. | |
| 7/A.M1 | Find accurately the graphical and analytical differential calculus solutions and, where appropriate, turning points for each type of given routine and nonroutine function and compare the results. | |
| 7/A.P1 | Find the first and second derivatives for each type of given routine function. | |
| 7/A.P2 | Find, graphically and analytically, at least two gradients for each type of given routine function. | |
| 7/A.P3 | Find the turning points for given routine polynomial and trigonometric functions. | |
| Sources of information to support you with this Assignment | mathsisfun.com/index.htm mathcentre.ac.uk/students/topics | |
Are You Searching Answer of this Question? Request British Writers to Write a plagiarism Free Copy for You.
BTEC Assignment Brief B
| Qualification | Pearson BTEC Level 3 National Extended Diploma in Electrical/Electronic Engineering |
| Unit number and title | Unit 7: Calculus to solve engineering problems |
| Learning aim(s) (For NQF only) | B: Examine how Integral calculus can be used to solve engineering problems |
| Assignment title | Solving engineering problems that involve integration |
| Assessor | Samira Shadbakht Mahani |
| Issue date | 27/11/2025 |
| Hand in deadline | 16/12/2025 |
Vocational Scenario or Context
You are working as an apprentice engineer at a company involved in the research, design production and maintenance of bespoke engineering solutions for larger customers.
Part of your apprenticeship is to spend time working in all departments, however a certain level of understanding needs to be shown before the managing director allows apprentices into the design team and so she has developed a series of questions on integration to determine if you are suitable.
Task 1
1 The tasks are to:
a) Find the indefinite integral of the function
* y = 3t² + 2e³ᵗ + 1/t + 2 cos 3t
b) Calculate the definite integral
∫₁² [3t² + 2e³ᵗ + 1/t + 2 cos 3t] dt
2 An object is moving with a uniform acceleration a = 2 ms⁻²,
determine the functions for:
a) Velocity v (ms⁻¹) – given v(0) = 10 ms⁻¹
b) Displacement s (m) – given s(0) = 5 m
c) Calculate the values of v and s for:
i) t = 2 s
ii) t = 5 s
3 The extension, y, of a material with an applied force, F, is
given by y = e⁽ᶠ×1×10⁻³⁾.
a) Calculate the work done if the force increases from
100 N to 500N using:
i) An analytical integration technique
ii) A numerical integration technique
[Note: the work done is given by the area under the curve]
b) Compare the two answers
c) Using a computer spreadsheet increase the number of values used for your numerical method
d) Analyse any affect the size of numerical step has on the result.
4. For the function y = 12 sin 4θ, calculate the:
a) Mean
b) Root mean square (RMS)
Over a range of 0 ≤ θ ≤ π/4 radians.
[Note the trigonometric identity cos 2θ = 1 – 2 sin² θ]
5. A complex function can be modelled by the equation:
y = cos(x³) 3x²
Find the indefinite integral of the function
∫ cos(x³) 3x² dx using a substitution method.
6. The acceleration of an object moving in a strange way has been modelled as a = e⁽ᶠˣ⁾.
a) Use integration by parts to find an equation to model the velocity if v = ∫ x e⁽ᶠˣ⁾ dx.
b) Is the problem any different if you find v = ∫ e⁽ᶠˣ⁾ dx?
7. Newton’s laws of cooling proposes that the rate of change of temperature is proportional to the temperature difference to the ambient (room) temperature. And can be modelled using the equation:
dT/dt = –k(T – Tₐ)
This can also be written as:
dT / (T – Tₐ) = –k dt
Where:
T = Temperature of material
Tₐ = Ambient (room) temperature
k = A cooling constant
Checklist of Evidence Required
Your informal report should contain:
- analysis
- worked solutions to the problems
Each worked solution should be laid out clearly and contain brief explanations of the stages of the calculation to indicate your understanding of how calculus can be used to solve an engineering problem. Graphs should be well presented and clearly labelled and comparisons between methods should be accurate and well presented.
Criteria Covered by this Task:
| Unit/Criteria reference | To achieve the criteria you must show that you are able to: | |
| 7/B.D1 | Evaluate, using technically correct language and a logical structure, the correct integral calculus and numerical integration solutions for each type of given routine and non-routine functions, including at least two set in an engineering context. | |
| 7/B.M2 | Find accurately the integral calculus and numerical integration solutions for each type of given routine and non-routine function, and find the properties of periodic functions. | |
| 7/B.P4 | Find the indefinite integral for each type of given routine function. | |
| 7/B.P5 | Find the numerical value of the definite integral for each type of given routine function. | |
| 7/B.P6 | Find, using numerical integration and integral calculus, the area under curves for each type of given routine definitive function. | |
| Sources of information to support you with this Assignment | http://www.mathsisfun.com/index.htm | |
| Other assessment materials attached to this Assignment Brief | ||
Get Solution of this Assessment. Hire Experts to solve this assignment for you Before Deadline.
Get Solution of this Assessment. Hire Experts to solve this assignment for you Before Deadline.
Assignment Brief C
| Qualification | Pearson BTEC International Level 3 Extended Diploma in Engineering
Pearson BTEC International Level 3 Extended Diploma in Electrical/Electronic Engineering Pearson BTEC International Level 3 Extended Diploma in Mechanical Engineering Pearson BTEC International Level 3 Extended Diploma in Digital Engineering Pearson BTEC International Level 3 Extended Diploma in Manufacturing Engineering Pearson BTEC International Level 3 Extended Diploma in Aeronautical Engineering |
| Unit number and title | Unit 7: Calculus to solve engineering problems |
| Learning aim(s) | C: Investigate the application of calculus to solve a defined specialist engineering problem |
| Assignment title | Investigate an engineering problem using calculus |
| Assessor | |
| Issue date | |
| Hand in deadline |
Vocational Scenario or Context
You are working as a Junior Engineer for a small motor racing team. You have been given a proposed mathematical model to calculate the velocity of a car accelerating from rest in a straight line. The equation is:
is the instantaneous velocity of the car (m/s) t is the time in seconds is the time to reach the maximum speed in seconds A is a constant.
The Team Manager has asked you to carry out an analysis of the model and produce a written report. As part of the analysis you have been given some data on a known model.
Task 1
Produce a report that contains written descriptions, analysis and mathematics that shows how calculus can be used to solve an engineering problem. The tasks are to:
- Use thinking methods to analyse the given engineering problem, e.g. break the problem down into a series of manageable elements, and produce a specification
- Prepare a valid proposal for solving the problem and present it
- Produce mathematical models for the identified elements of the problem
- Apply calculus methods to produce answers for each of the elements
- Bring the elements together in a formal presentation
In your proposal you need to outline the problem and the methods needed to solve it. You need to include how to
(1) Identify the
-
- units of the coefficient A
- physical meaning of A
- velocity of the car at t = 0
- asymptote of this function as t → ∞?
- (2) Sketch a graph of velocity vs. time.
(3) Derive an equation x(t) for the instantaneous position of the car as a function of time. Identify the
-
- value x when t = 0 s
- asymptote of this function as t → ∞
(4) Sketch a graph of position vs. time.
(5) Derive an equation for the instantaneous acceleration of the car as a function of time.
Identify the
- acceleration of the car at t = 0 s
- asymptote of this function as t → ∞
(6) Sketch a graph of acceleration vs. time.
(7) Apply your mathematical models to your allocated car. Use the given data for the 0 – 28 m/s and 400m times to calculate the:
-
- value of the coefficient A
- maximum velocity
maximum acceleration.
Checklist of evidence required
Your informal report should contain:
- written descriptions,
- analysis
- worked solutions to the problems
Each worked solution should be laid out clearly and contain brief explanations of the stages of the calculation to indicate your understanding of how calculus can be used to solve an engineering problem. Diagrams and sketches should be well presented and clearly labelled.
Criteria covered by this task: |
||
| Unit/Criteria reference | To achieve the criteria you must show that you are able to: | |
| 7/C.D3 | Critically analyse, using technically correct language and a logical structure, a complex engineering problem, synthesising and applying calculus and a mathematical model to generate an accurate solution. | |
| 7/C.M3 | Analyse an engineering problem, explaining the reasons for each element of the proposed solution | |
| 7/C.M4 | Solve accurately, using calculus methods and a mathematical model, a given engineering problem. | |
| 7/C.P7 | Define a given engineering problem and present a proposal to solve it | |
| 7/C.P8 | Solve, using calculus methods and a mathematical model, a given engineering problem | |
| Sources of information to support you with this Assignment | mathsisfun.com/index.htm mathcentre.ac.uk/students/topics | |
| Other assessment materials attached to this Assignment Brief | Table of 0-28 m/s, 400m and time to reach maximum speed times. | |
Stuck in Completing this Assignment and feeling stressed ? Take our Private Writing Services
Struggling with the complex calculus tasks in Unit 7—differentiation, integration, modelling or engineering optimisation? Whether you’re working through Assignment A, B or C, many engineering learners find these calculus problems time-intensive and difficult to structure correctly. Our UK engineering specialists provide clear, accurate and 100% human-written BTEC solutions, including full working, graphs, explanations and professionally formatted reports. View our BTEC Engineering Assignment Samples, or get personalised support through our BTEC Level 3 Engineering Assignment Help to score higher with confidence.