BTEC Level 4 Unit 2 (M/615/1476 ) Mathematical and Statistical Applications in Engineering Assignment 1: Dimensional Analysis to Quality Control
| University | Walsall College |
| Subject | Unit 2 (M/615/1476) Engineering Maths |
Relevant Learning Outcomes and Assessment Criteria
| Pass | Merit | Distinction | |
|---|---|---|---|
| LO1 Identify the relevance of mathematical methods to a variety of conceptualised engineering examples | P1 Apply dimensional analysis techniques to solve complex problems. P2 Generate answers from contextualised arithmetic and geometric progressions. P3 Determine solutions of equations using exponential, trigonometric and hyperbolic functions. |
M1 Use dimensional analysis to derive equations | D1 Present data in a method that can be understood by a non-technical audience |
| LO2 Investigate applications of statistical techniques to interpret, organise and present data | P4 Summarise data by calculating mean and standard deviation P5 Calculate probabilities within both binomially distributed and normally distributed random variables |
M2 Interpret the results of a statistical hypothesis test conducted from a given scenario |
Unit Learning Outcomes
- LO1: Identify the relevance of mathematical methods to a variety of conceptualised engineering examples.
- LO2: Investigate applications of statistical techniques to interpret, organise and present data.
Are You Searching Answer of this Question? Request British Writers to Write a plagiarism Free Copy for You.
Assignment Brief and Guidance
Scenario:
You work as a Test Engineer for a global manufacturer of electrical and mechanical components and systems. Your Line Manager is responsible for delegating to you and your colleagues the testing of theory, principles, and hypotheses from several worldwide company divisions. They have asked you to undertake a series of such evaluations.
Activity:
Part 1:
a) The potential energy of a mass, m, held at a particular height, h, above the ground against the force of gravity, g, is converted into kinetic energy when it is released and it moves towards the ground at a velocity, v.
Use dimensional analysis to confirm the relationship:
mv2/2 = mgh
b) It is postulated that the force acting on a body moving in a circular path is proportional to its mass, m, velocity, v, and radius, r, as follows:
F ∝ m v r
Use dimensional analysis to confirm the relationship and develop a final formula for the force, F.
c) An analogue-to-digital converter (ADC), manufactured by your signals division, records hundreds of voltage samples of a linear waveform, measured in mV, for quality assurance purposes. The samples commence as 5, 8, 11, 14, 17………etc.
Your test colleague has asked you to assist by determining a formula that describes the sequence in terms of the nth term of that sequence, and then to use that formula to determine the value of the 372nd sample, which has failed to be recorded correctly.
The final stage of the process requires the summation of all samples up to and including the 372nd sample. Determine a formula to produce the result of this summation.
d) A digital chip, made by your Microelectronics division, counts continuously in the sequence:
32, 64, 128, 256, …
You have been asked to determine a formula to calculate the nth count of the chip. Now apply your formula to work out the value of the 15th count.
e) A series electrical circuit for a funfair arcade machine which you are testing, features a capacitor (C) charging via a 1 MΩ resistor (R) and a DC supply voltage (Vs). The voltage across the capacitor (Vc) may be described by the following equation, where t represents time.
vc = vs(1 – e-t/RC)
The arcade machine produces an output based upon the year of your birth, which is input at the start of the game, by changing the value of the DC supply voltage (Vs). For example, if you were born in 1994 then Vs = 1 + 9 + 9 + 4 = 23 V.
Assuming that Vc is 1V after a time of 3 seconds, determine the approximate value of the capacitor.
f) One of your commonly used laboratory instantaneous test signal voltages (vs) is described by the equation…
vs = 5sin(2πft – π/3)
where f = 1MHz and t represents time.
Make time (t) the subject of this formula, and hence determine the first point in time when the instantaneous signal voltage has a magnitude of +3V.
Note: A colleague has reminded you that you need to have your calculator in radians mode (RAD) for this calculation, because the angle is given in radians (i.e. π is featured).
Use this software or this software to draw at least two cycles of this signal and annotate the drawing so that your non-technical colleagues may understand the relevant information it contains.
g) The curve assumed by heavy power cables manufactured by your Power division, and suspended between electricity pylons, is called a catenary, and is described by the equation…
y = 50 cosh(x/50)
Your Line Manager has asked you to calculate:
(i) the value of y when x = 60
(ii) the value of x when y = 150
Get Solution of this Assessment. Hire Experts to solve this assignment for you Before Deadline.
Part 2:
a) Your manufacturing division produces resistors with a nominal value of 22 kΩ, with a tolerance of +/- 10%. A random sample of ten resistors was taken, and their value was measured by a colleague, to check that they remain within tolerance. The results are as follows:
| Sample | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|
| Resistance (kΩ) | 22.8 | 21.7 | 20.5 | 23.1 | 22.8 | 21.7 | 22.4 | 23.2 | 21.7 | 22.8 |
(i) Calculate the mean resistance for these samples.
(ii) Determine the standard deviation for the samples.
(iii) Produce a Tally Chart showing the frequency of measured resistances.
b) Further analysis of a larger sample of the resistors shows that 90% are within the allowable tolerance value. The remainder exceed the tolerance. You select eight resistors at random from the sample. Determine the probabilities that:
(i) Two of the eight resistors exceed the tolerance.
(ii) More than two of the eight resistors exceed the tolerance.
c) Your analysis shows that the mean resistance of a batch of 500 of the resistors you have selected is 21.5kΩ, with a standard deviation of 2kΩ. Assuming the resistors are normally distributed, determine the number of resistors likely to have values between 19kΩ and 24kΩ.
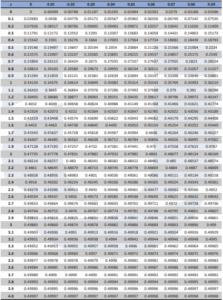
Note: Use the z-table given in Appendix A when answering part c.
d) The Quality Assurance Department is anxious to improve the nominal value of the resistors to ensure more of them fall within the rated tolerance band. The manufacturing process is adjusted in an attempt to bring about this improvement. Following the adjustment, a further sample of 100 resistors is taken in order to determine if the adjustment has resulted in an improvement to the nominal value of the resistors. Analysing this second sample, it is noted that the mean value is now 21.8kΩ, with a standard deviation of 1kΩ.
By comparing these new results of the resistor values following the manufacturing adjustment, with the values obtained in part (c) recorded before the adjustment, show whether or not you agree with the hypothesis that the adjustment to the manufacturing process has had a beneficial effect by making the resistor values closer to the desired manufactured nominal value of 22kΩ.
Illustrate your answer with a hand drawn sketch of the normal distribution, with shaded regions representing the results of your analysis, which you can show to the Quality Assurance Manager.
Note: Use the z-table given in Appendix A when answering part d.
Appendix A
Stuck in Completing this Assignment and feeling stressed ? Take our Private Writing Services