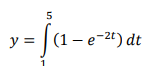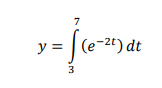BTEC Level 4 Unit 2 (M/615/1476 ) Engineering Maths Assignment 3: Differentiation, Integration & Curve Analysis for Dynamic Electrical Systems

Relevant Learning Outcomes and Assessment Criteria

LO4 Examine how differential and integral calculus can be used to solve engineering problems

P8 Determine rates of change for algebraic, logarithmic and circular functions.

P9 Use integral calculus to solve practical problems relating to engineering.

M4 Formulate predictions of exponential growth and decay models using integration methods

D3 Analyse maxima and minima of increasing and decreasing functions using
higher order derivatives.

Assignment Brief and Guidance

Scenario:

You work as a Test Engineer for a global manufacturer of electrical and mechanical components and systems. Your Line Manager is responsible for delegating to you and your colleagues the testing of theory, principles,
and hypotheses from several worldwide company divisions. They have asked you to undertake a series of such evaluations..

Activity

Task 1:

Differentiate each of the following current functions with respect to time and hence determine the ‘rate of change’ for each of the functions when time, t, is 3 seconds.

a) 𝑖𝑖 = (3𝑡𝑡 + 5)4
b) 𝑖𝑖 = (4𝑡𝑡3 − 2𝑡𝑡 + 3)3
c) 𝑖𝑖 = 𝑙𝑙𝑙𝑙𝑙𝑙𝑒𝑒(3𝑡𝑡2)
d) 𝑖𝑖 = 2𝑒𝑒(3𝑡𝑡+4)
e) 𝑖𝑖 = sin(5𝑡𝑡3 + 6𝑡𝑡 − 3

Task 2:

PART 1

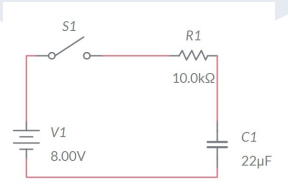
For the circuit shown below, assuming zero charge on the capacitor at t = 0, the current flowing may be quantified as:

Integrate this equation with respect to t and hence find the charge stored in the capacitor 0.5 seconds after the switch is closed.

PART 2
The current (𝑖𝑖𝐿𝐿) through a 100 mH inductor (L) has a relationship with time (t) as follows:

Determine the inductor current when the time is 0.75 seconds

Task 3:

PART 1
Determine the area under the following exponential growth curve between 1 seconds and 5 seconds:

PART 2
Determine the area under the following exponential decay curve between 3 seconds and 7 seconds:

Task 4:

PART 1
Locate the co-ordinates of the turning point for the following function and determine whether it is a maxima or minima:

PART 2
Find the maxima and minima values for the function: